计算机图形学

掌握计算机图形学的基本概念，理解光栅图形生成基本算法。理解三个常用直线生成算法，理解和掌握多边形的扫描转换、区域填充算法。掌握曲线的概念，曲线曲面的表示。掌握 Bezier 曲线、B 样条曲线、非均匀有理 B 样条曲线的定义和性质、算法。理解颜色的基本概念、三色学说、CIE 色度图、掌握常用的颜色模型，掌握光照相关知识，掌握几种基础光照模型，理解光线跟踪算法。熟悉 OpenGL 程序结构、基本几何元素、坐标变换和光照处理。

图形学概论

图像 vs 图形

图像	图形
简单，相机，真实的	复杂，由算法生成，是合成的
表示：用像素阵列表示	表示：几何属性 + 物理属性
像素有颜色值 (或灰度值)	需要人来设计和构造

生成的图形

线框图	真实感图形	非真实感图形
用线条表示	侧重真实感	侧重艺术、风格化

帧缓存

作用：存储将要显示的图形信息和保存中间数据。

包括：颜色缓存和深度缓存等。

显存与 GPU 的关系，就像内存和 CPU 的关系一样。

图形学之父

I.E. Sutherland

二维集合变换

概念

坐标系不动，把一个图形通过平移、旋转、缩放、对称、错切变换变成新的图形。

1. 对简单图形作变换和组合，可以构成复杂图形，是造型的方法之一。

2. 三维变换的基础。

基本变换

平移变换

性质：只改变位置，不改变形状和大小。

旋转变换

性质：不改变大小、距离和角度，会改变朝向

缩放变换

当 Sx == Sy 时为均匀缩放，反之为非均匀缩放。

性质：

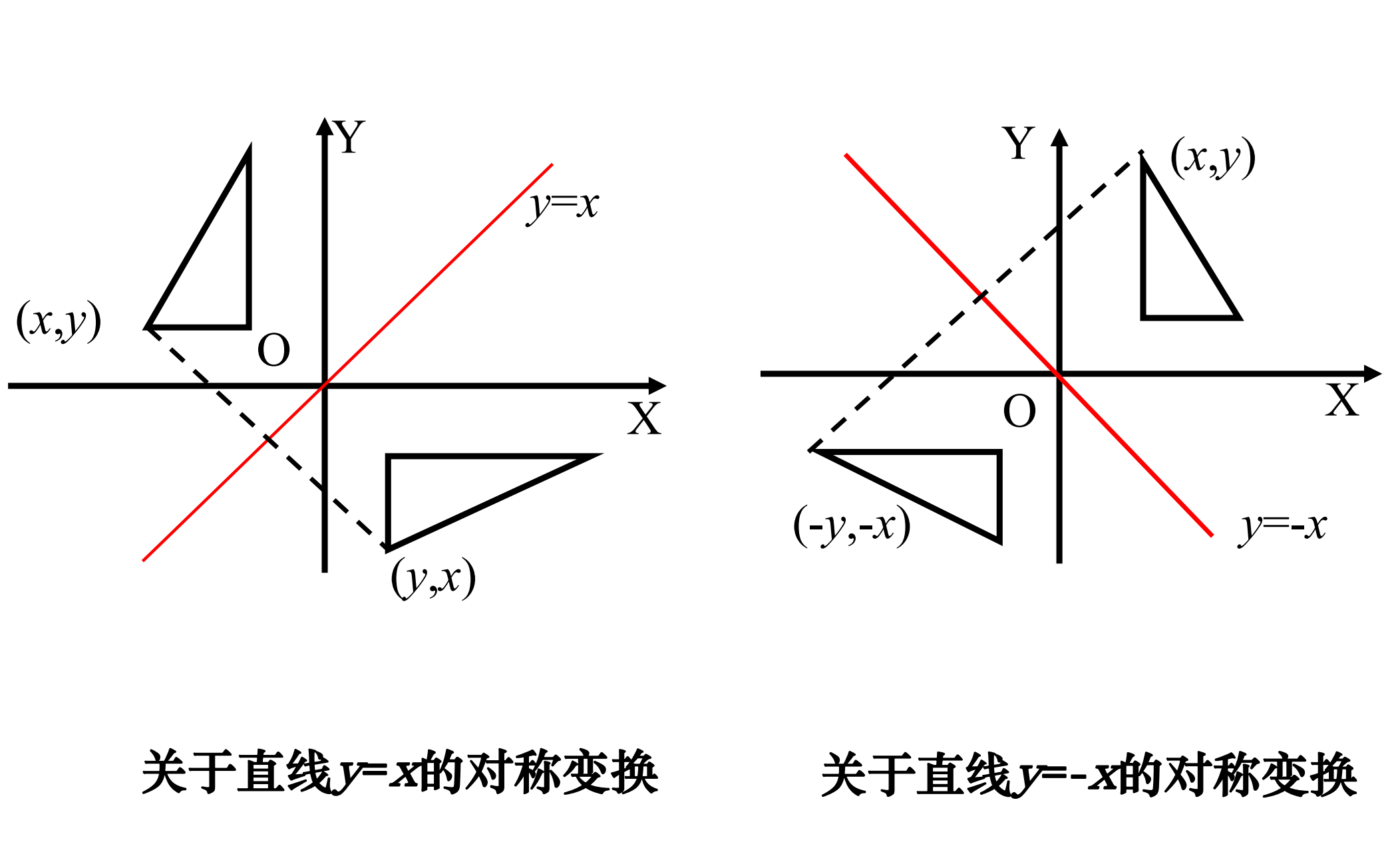
对称变换

关于 x 轴，y 轴，原点的对称变换是特殊的缩放变换。

逆变换

正变换：从 P(x,y) 变到 P’(x’ ,y’)

逆变换：从 P’(x’ ,y’) 变回 P(x,y)

复合变换

• 复合平移

• 复合旋转

• 先平移，再旋转，再缩放

• 先旋转，再平移，再缩放

• ...

性质：复合变换不满足可交换性

关于参考点旋转

相对某个参考点 (xr,yr) 的旋转变换：

(1) 作平移

(2) 作相对原点的旋转

(3) 作反平移

矩阵乘向量

齐次坐标

把 n 维空间的点表示成 n + 1 维空间的点，称前者为普通坐标，后者为齐次坐标。

齐次坐标不唯一

(1,3,0) 的齐次坐标是 (2,6,0,2)、(1.5,4.5,0,1.5) —— 不唯一。

普通坐标与齐次坐标的关系

规范化齐次坐标

h=1 时的齐次坐标成为规范化齐次坐标。

矩阵乘向量

三维图形变换

坐标系不动，点动。

特点：

1. 比 2D 增加了 z 坐标

2. 比 2D 更复杂、更真实

三维几何变换性质：

• 平移——改变位置

• 旋转——改变方向

• 缩放——改变大小和形状

• 对称

• 错切

平移变换

只改变位置，不改变大小和形状。

旋转变换

绕三个坐标轴的旋转

绕 z 轴旋转：约定人眼在 z 轴正方向，看向原点，逆时针为正方向

绕三个坐标轴正方向旋转

绕任意轴的旋转

eg.

投影变换

数学上：从 n 维空间到 k(<n) 维空间的变换。 CG：从 3D 空间到 2D 平面的变换。

物体在 3D 空间，屏幕在 2D 平面，必须作投影变换。投影变换是 3D 图形学的核心。

基本概念

投影中心：相当于人眼或相机，也称视点或观察点 投影线：相当于光线 投影面：相当于成像平面，位于 COP 和物体之间 投影线与投影面相交，在投影面上的像就是物体的投影。

光学成像 vs 虚拟成像

透视投影 vs 平行投影

透视投影：COP 到投影面的距离有限 平行投影：COP 到投影面的距离无限

平行投影是透视投影的极限

平行投影

类比太阳光

三视图

性质：保持距离和角度不变，适用于建筑和施工图纸。

三视图的变换公式

正轴测投影

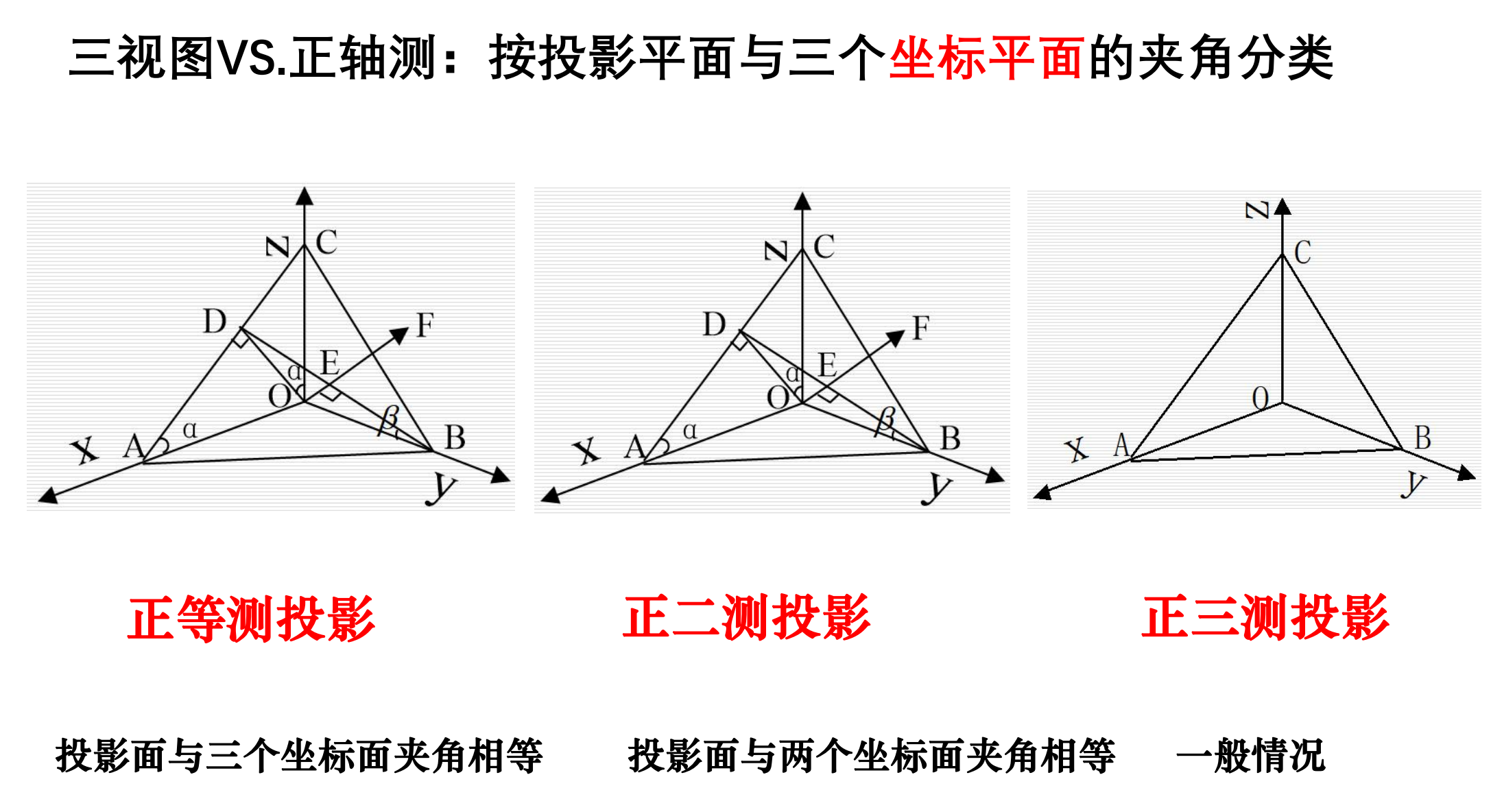
缺点

物体投影的大小与物体离投影面的距离无关，与人的视觉不符。

透视投影

符合人的视觉特点，远小近大，更真实

性质：平行于投影面的平行线投影后仍然平行。不平行于投影面的平行线投影后汇聚于一点。

透视投影变换公式

坐标系

建模坐标系

1. 三维坐标系，坐标在 R 上取值

2. 目的：用来定义单个物体，比如球体，长方体，圆柱体。。。

3. 每个物体都可以有自己的建模坐标系。MC 是局部坐标系，如果物体改变，MC 也随之改变。

世界坐标系

1. 三维坐标系，坐标在 R 上取值

2. 目的：定义所有对象，包括物体，观察者的位置和视线、投影平面等。

3. 是全局坐标系，其它坐标系都参照 WC 来定义。

观察坐标系

1. 目的：从观察者的角度描述 WC 中的所有物体。

2. 类比照相：选择拍摄的位置和方向。

3. 对同一场景，在不同视点处的观察结果不同。

投影面坐标系

设备坐标系

1. 设备自带的坐标系。设备不同，设备坐标系也不同。

2. 二维坐标系，取离散值，比如 1024 * 768，1920 * 1080。

规范化设备坐标系

1. 二维坐标系，在 0≤X≤1，0≤Y≤1 取连续值。

2. 目的：为了解决应用程序的可移植性的问题，使图形处理独立于具体的输出设备。

3. 虚拟的设备坐标系。

多边形的扫描转换

把顶点表示转换为点阵表示

本质：给定多边形的顶点序列，确定哪些像素在多边形内部。

多边形的表示

顶点表示	点阵表示
用顶点序列表示。	用多边形内部的像素表示。
优点：几何意义明显，直观，存储空间少，便于作几何变换。	优点：适用于面着色。
缺点：不能直接进行面着色。	缺点：失去顶点、边界等几何信息，存储空间多，不便作几何变换。

点的包含性检验

转角法

缺点：逐点判别，计算夹角的大小和方向

射线法

看奇偶：如果交点个数是偶数（包括 0），则点在外面；否则在里面。

缺点：逐点判别，需要判断一条射线和所有边是否有交点

扫描线填充算法

1．求所有顶点的 MIN 和 MAX——确定多边形覆盖的扫描线条数 2．从 MIN 到 MAX，每次用一条扫描线进行填充

1. 求交：依次计算该扫描线与各边的交点；

2. 排序：把所有交点按 x 值递增排序 (比如冒泡)；

3. 配对：第 1 与第 2，第 3 与第 4，每对交点确定一个小区间；

4. 填色：把小区间内的像素赋予颜色。

如何避免不必要的求交

增量法求交点坐标

扫描线的连贯性

如果没有新边加入，排序不变，无须调整

如果有新边 (第一次与扫描线相交的边) 加入，可用插入排序

交点为顶点的配对

顶点分三种：极小点，极大点，其它点。

避免填充扩大化

活性边表

活性边：对一条扫描线，和扫描线有交点的边。 活性边表：对一条扫描线，把所有活性边按 x 坐标递增的顺序构成一个链表。 链表结点 = data 域 + 指针域。

新边表

对每条扫描线建立表，用来存放与该扫描线第一次相交的边 (新边) 结点结构和活性边表相同。

区域填充

区域：连通的像素集合。

区域表示

区域分类

字符

包括字母、数字、汉字等。是特殊的图形，用于图形的注释说明等。

字符编码

美国：

• 信息交换用标准代码集 (American Standard Code for Information Interchange)

• 127 个字符，8 位编码

中国：

• 汉字编码的国家标准字符集：GB 2312－80。

• 区位码：对 6763 个常用汉字，符号等编码，94 个区，94 个位，

用 94 * 94 矩阵表示。

字符表示

点阵型

每个字符用一个点阵表示，1 表示笔画经过，0 表示不经过

缺点：

1. 字符有多种属性——数据量很大

2. 作变换 (比如旋转) 困难（需要操作每个像素）

压缩技术：

黑白段压缩、部件压缩、轮廓字形压缩

轮廓字形：

用直线、2/3 次 Bezier 曲线描述轮廓线，轮廓线构成区域的边界。用填充算法生成字符的点阵。优点：压缩比大，能保证字符质量。

矢量型

不记录点阵，而是记录字符的笔画。

把字符表示成点的序列，相邻两点构成一个矢量，字符的形状由矢量序列表示。

优点：存储空间小，变换方便，只需对端点坐标作变换

基本图形生成算法

什么是生成

CG 是研究如何用计算机表示、生成、处理和显示图形的学科。

扫描转换：把图形数据转换成像素。

本质：给定图形，在屏幕上确定最佳逼近图形的像素。

直线的表示方法

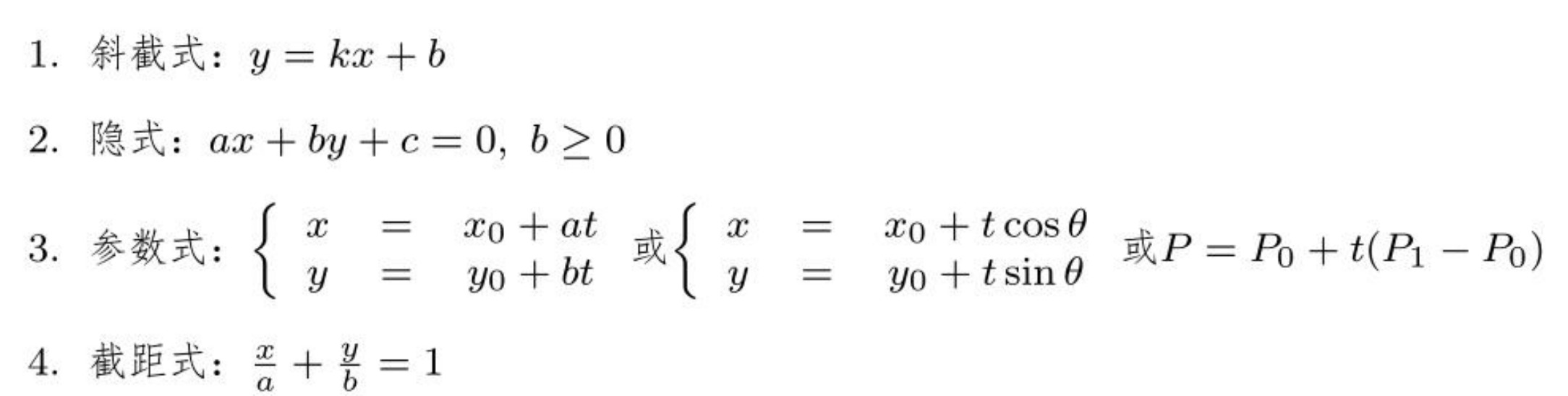
点和直线的位置关系

判别式 & 判别规则

直线的扫描转换

数学：直线是理想 (绝对直) 的，由无数个点构成，没有宽度。

计算机：有限个点，有宽度

本质：用有限的像素逼近理想直线

直接计算法

DDA 算法

优点：增量算法

缺点：k、y 是 float，需要作浮点乘法，对 y 作舍入，不利于硬件实现

中点画线法

判别式与判别规则

判别式改进 —— 用增量法计算 d

判别式改进 —— 用 2d

裁剪

裁剪：给定窗口，消除窗口以外的部分。

为什么要作裁剪：场景太大，需要显示的只是整个场景的一部分。

流程：先裁剪，再光栅化，避免无用的计算。

裁剪分类

1. 裁剪窗口的维数

• 2D、3D

1. 裁剪窗口的形状

• 规则 (矩形、圆)

• 不规则 (多边形、多面体)

1. 裁剪对象

• 点、线、多边形、字符

点裁剪

线裁剪

Cohen-Sutherland 算法

![[Pasted image 20231226210109.png]]

优点

• 解决前两种很高效，避免了不必要的求交

• 适合大窗口和小窗口

缺点

• 求交涉及浮点运算

• 最坏的情况需要作四次裁剪

反走样

用离散量 (像素) 表示连续量 (图形) 引起的失真。

走样是数字化的必然产物。减少或消除走样称为反走样。

常见的走样

• 锯齿形或阶梯形

• 小物体、细节在被放大、丢弃、失真

• 小物体在动画中时隐时现，产生跳跃或闪烁

反走样技术

• 硬件：提高分辨率

增加分辨率，减轻锯齿效应，原来不能显示的细节可以显示。

4 倍帧缓存容量和 2 倍扫描时间——成本太高

• 算法

利用亮度过渡淡化锯齿效应。

区域采样

消隐

消除不可见的点线面，称作消隐。

在 3D 中，人从某视点观察，不可能看到一个物体的全部表面，只能看到部分的点线面。若观察多个物体，物体之间还存在彼此遮挡。

消隐分类

1. 按消隐对象

• 线消隐：针对线框图，消除边

• 面消隐：针对表面图，消除面

1. 按算法所在空间分类 (Southerland)

• 物体空间 (object space)

• 图像空间 (image space)

• 二者结合

影响因素

几乎所有算法都会涉及远近排序

物体离视点越远，越可能被遮挡 物体离视点越近，越可能被看见——近的遮挡远的

连贯性 a. 扫描线的连贯性 b. 物体的连贯性

物体空间方法

for (每个物体)
{
把它与其它物体比较，确定可见的部分；
用适当的颜色绘制可见部分；
}

图像空间方法

1. 在 2D 空间 (屏幕坐标系) 进行

2. 处理对象：投影后的像素

3. 复杂度：n 个对象，m 个像素，需做 m * n 次求交。

for(屏幕上的每个像素)
{
比较深度，确定哪个多边形在该像素可见（离视点最近）；
绘制该像素；
}

相结合：先在物体空间删掉一些不可见的面，再在图像空间生成消隐图。

面消隐

画家算法

与油画家作画类似，由远及近，远景覆盖背景。

1. 把物体按远近（或深度）排序。

2. 按由远到近的顺序依次绘制各个面（后者覆盖前者）。

Z-buffer 算法（深度缓存算法）

图像空间方法

算法步骤

z 值计算

增量算法

优缺点

优点

• 思想简单

• 物体不用排序

• z 值可用增量法求出

缺点

• 占用空间大，需要两个缓存。

• 本质上是逐点，没有充分利用连贯性。

区间扫描线算法

利用扫描线的连贯性，以区间为单位确定可见区域。

对每条扫描线，计算它和所有多边形投影的交点，按交点排序，形成若干小区间。

算法步骤

1. 没有多边形覆盖 ——用背景色显示 。

2. 只有一个多边形覆盖——用该多边形的颜色显示 。

3. 两个或以上覆盖——比较深度，用可见多边形的颜色显示 。

算法特点

1. 一次可以确定一个区间

2. 不需要 z 缓存

Wornack（区域细分）算法

特点

• 图像空间方法

• 思想：分而治之

• 区域连贯性 (对比扫描线连贯性)

如果一点可见，则周围的点也可见。 如果一点不可见，则周围的点也不可见。

多边形和窗口的关系

• 不相交 —— 分离

• 内含

• 包围

• 相交

定义简单窗口：

1. 所有多边形都和窗口分离——窗口为背景色

2. 窗口中只包含一个多边形

3. 只有一个多边形包围窗口

4. 只有一个多边形和窗口相交

5. 有多个和窗口相交，但是，有一个包围窗口，而且离视点最近

算法步骤

1. 把所有多边形投影到窗口。

2. 检查窗口是否简单。如果简单，结束。

3. 否则，把窗口一分为四，检查窗口是否简单。

4. 终止条件：所有窗口简单，或者窗口只含一个像素。

光线投射算法

a. 视点和像素形成射线。 b. 射线与所有物体表面求交。 c. 取离视点最近的交点。

算法过程

for (屏幕上的每一像素(u,v) {
	形成通过该像素(u,v)的射线；
	for (每个多边形) {
		射线与该物体表面求交；
		if 存在交点
			以最近交点的颜色显示像素(u,v)
		else
			以背景色显示像素(u,v)
	}
}

光线投射法 vs Z-buffer 算法

1. 内外循环顺序相反，所以算法复杂度类似。

Z-buffer：每次取一个多边形，作投影，对投影点计算深度值，将其与已有的深度值作比较，取最近的那个。

光线投射法：每次取一个像素，沿光线路径计算所有面的深度，取最近的那个。

1. 光线投射法不需要 Z 缓存。

曲线与曲面

曲线/曲面的分类

1. 规则

• 可用初等解析函数表示 • 直线，圆弧，椭圆，平面，球面，椭球面

1. 自由

• 无法用初等解析函数表示 • 汽车外形，飞机外形

1. 随机

• 处处连续，处处不可导 • 地图边界，海岸线，水波，超声

曲线和曲面的表示

平面曲线的表示

点动成线：曲线可看成动点运动的轨迹，t 表示时间，角度等。直线 [0, 1] 弯曲的结果。

规范化参数区间 [0, 1]

若 t 的区间是 [a, b]，转换为 [0, 1]

t’ = (t - a) / (b - a)

则 t’ => [0,1]。

第一象限内的单位圆弧

直线

三类表示优缺点

• 显式表示

缺点：

1. 不能表示竖线

2. 不能表示多值或封闭曲线（如整圆）

• 隐式表示

优点：

1. 能表示任意直线、整圆

2. 将某点坐标代入隐式，可判断该点在曲线的哪一侧

缺点：

1. 由 x 难计算对应的 y

• 参数表示

优点：

空间曲线的表示

参数曲面

上半单位球面

平面法向量

插值与拟合

插值

给定 n+1 个有序的点 Pk，k=0, 1, …, n，构造一条曲线顺序通过它们，称为对这组数据点进行插值，曲线称为插值曲线。

线性插值

抛物线插值

n+1 个点，n 次插值

拟合

给定一组数据点，构造一条曲线，使它在某种意义下最接近这些数据点 (未必通过)，该曲线称为拟合曲线。

3 次参数曲线

为什么选 3 次

• 次数太低，不灵活。

• 次数太高，计算量大，光滑性变差。

• 可以通过若干条 3 次曲线拼接得到复杂曲线。

连续性

复杂曲线通常由若干曲线段拼接而成，要保证曲线段之间光滑过渡的问题。

参数连续性

例子

几何连续性

Bezier 曲线和曲面

Bezier 曲线

一次 Bezier 曲线

二次 Bezier 曲线

三次 Bezier 曲线

Bernstein 基函数的性质

端点性质

曲线经过第一个和最后一个控制点（利用基函数的端点性质）

导数性质

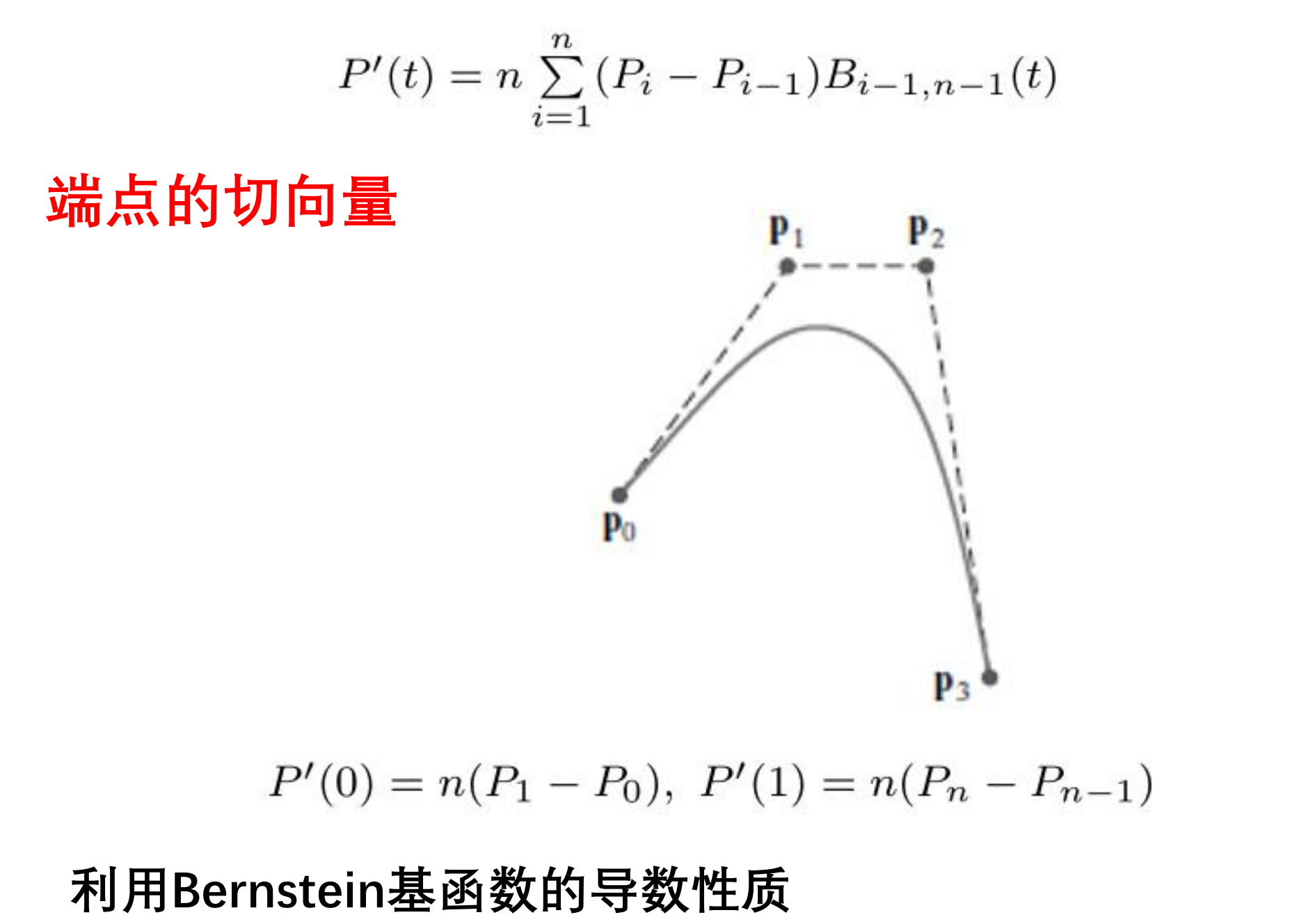
二阶导性质

凸包性

变差缩小性

任意直线与曲线的交点个数小于等于该直线与多边形交点的个数。

Bezier 曲线比控制多边形波动更小。

对称性

Bezier 曲线的递推

Bezier 曲线的拼接

Bezier 曲线的性质

没有局部可控性：如果改变某一个控制点的位置，整条曲线都会变化。

在 (0,1) 上，每个基函数均>0。

Bezier 曲面

真实感图形学

颜色

颜色是视觉系统对可见光的感知结果。

光

光是一种电磁波。

大多数彩色光不是单一波长的，而是由许多不同波长的光组合成的。

缺点：

1. 用光谱能量分布定义颜色非常复杂，难以理解。

2. 因为异谱同色，所以对人没有必要。

3. 计算机难以处理。

光谱和颜色是多对一的，不同分布的光产生的颜色感觉是一样的，两种光的分布不同但是颜色相同的现象称为异谱同色。

颜色模型

表示颜色的一种数学方法。颜色模型不是唯一的。

• 存储（R,G,B 值）

• 减少数据量（压缩）

• 满足显示系统的要求

• 满足印刷或打印的要求

• 方便用户理解和选择颜色

没有任何一个颜色模型能解释有关颜色的所有现象。只能近似地解释。

有源物体

能发出光波的物体称为有源物体，其颜色由它发出的光波决定。

无源物体

不发出光波的物体称为无源物体。其颜色由它吸收其它颜色的光后反射的光波决定。

定义物体的颜色：白光照射在它上面时显示的颜色。

RGB 模型

常见的各种颜色光，都可以由红 (R)、绿 (G)、蓝 (B) 三种颜色光按不同比例混合而成。

补色

数字图像表示

黑白图像

8-bit 灰度图像

只有明暗不同，没有色彩。8bit 灰度图。 共 256 种亮度

彩色图像

24-bit 彩色图像

通常用 8bit 表示每个颜色分量。

优缺点

优点：

1. RGB 可以生成很多的颜色

2. 适合硬件（图像生成）（e.g., 显示器、相机、扫描仪）

缺点：

1. 不直观（用户描述颜色不方便）

2. 很难编辑（视觉对颜色的感知是非线性的）

CMY（减色）模型

用青 (cyan)、品红 (magenta) 和黄 (yellow) 颜料按一定比例混合得到颜色的方法。

颜色不是来自光线的叠加，而是光线照射到颜料以后，被颜料吸收一部分后反射剩余的光线，称为 CMY 减色模型 (印刷模型)。

CMY 模型的表示

CMYK 模型

1. 油墨包含杂质，实际上产生一种深灰色

2. 直接加入黑色更经济

加入一种黑色 (K) ——四色打印

优点

1. CMY 可以生成很多颜色

2. 适用于印刷或打印

缺点

1. 颜色的生成方式不直观

2. 难以编辑（视觉对颜色的感知是非线性的）

HSV 模型

• 色调 (Hue, H)：即颜色。反映颜色的基本特征。色调是最容易把颜色区分开的属性。由光的主波长决定

• 饱和度 (Saturation)：颜色的纯正 (鲜艳) 程度。单一波长的光是完全饱和的。与掺入的白光有关：掺入白光，色调不变但饱和度降低。

• 亮度 (Value)：主观亮度，人眼感受到的颜色光的强度。某一颜色的光，亮度很弱，趋于黑色；亮度很强，趋于白色。

优点

1. 可以生成很多颜色

2. 符合人的主观感受

缺点

1. 与设备相关

总结

1. RGB，显示设备

2. CMY，打印或印刷

3. HSV，人

光照模型

根据光学定律，建立数学模型，计算物体表面每个点的颜色 (或亮度)。

光源模型要素

1. 光源

• 形状 (点、线、面、体)

• 位置（x,y,z）

• 发光方向（角度）

• 亮度或颜色 (光谱)

1. 物体

• 形状、表面朝向、材质、颜色、透明性

1. 视点

点光源

发光体很小或者相距很远，可视为点光源。

光强度衰减

设离光源距离为 d。光强度和距离的平方成反比。

局部光照模型 vs 全局光照模型

局部光照模型	全局光照模型
只考虑光源直接照射。	不仅考虑光源直接照射，也考虑间接照射。
目的：模拟连续明暗色调、镜面高光。	目的：模拟多个物体之间的反射、透射、物体交相辉映等。

简单光照模型

Phong 模型

反射光=环境光的反射光 + 漫反射光 + 镜面反射光

• 真实感图形学中第一个有影响的光照模型。

• 生成图像的真实感较好。

• 是一个经验模型。

• 环境光设为常量，没有考虑物体间相互的反射光。

• 物体像塑料，不生动，无质感

环境光

概念

• 又称为背景光 (background light)、泛光。

• 光源不能直接照射的地方，依然有一定的亮度。

• 看成光源间接对物体的影响，是光在物体和环境之间多次反射，最终达到平衡后，弥漫在整个空间。

只考虑环境光，物体没有立体感。类比黑夜里看东西，同一物体的不同区域无差异，只有位置、大小、轮廓。

特点

• 来自周围各个方向，均匀地向各个方向反射。

• 强度分布均匀，任何地方都一样，看成常数。

• 和物体的朝向、观察方向无关。

• 比如透过厚厚云层的太阳光，无影灯。

计算

漫反射

发生在粗糙表面，比如墙面。

特点：漫反射光均匀地向各个方向反射

环境光 + 漫反射，颜色 (亮度) 有过渡，但无光泽。

Lambert 余弦定律

与入射光的亮度、入射方向、材质有关。

入射光线的垂直分量才对照明有作用。

漫反射光强计算

设 L，N 为单位化向量。

镜面反射

发生在有光泽的表面，如擦亮的金属等。

只有当人眼恰好位于反射方向，才能感知亮度；否则不能。

高光

如果物体表面很光滑，且人眼在反射光线附近，那么反射光的大部分到达人眼，形成很亮的光斑。比如额头。

1. 物体表面越光滑，高光区越小，越亮。

2. 光斑的颜色由入射光颜色决定，不取决于物体的颜色。

非理想镜面反射

高光指数 n

Phong 镜面反射模型

环境光 + 漫反射 + 镜面反射

计算反射方向 R

Blinn-Phong 模型

对物体表面每个点 P，都需要计算 (L,N) 和 (V,R)。为了减少计算量，1977 年，Blinn 改进 Phong 模型。

明暗处理

平面绘制

1. 求多边形的法向 N

2. 任取一点 P，调用 Phong 模型计算 P 的亮度 I

3. 把 I 赋给多边形投影覆盖区域的所有像素

1. 一个多边形内部所有点亮度相同

2. 相邻的多边形亮度有跳跃

缺点：马赫带效应

马赫带效应 (Mach band effect)，1868 年奥地利物理学家马赫发现。马赫带效应不是物理现象，而是心理现象。 当观察两块亮度不同的区域时，边界处的亮度对比会加强，使轮廓特别明显。

解决方法：

1. 用更多的多边形逼近曲面，使得亮度跳跃小于人眼的分辨力 —— 多边形增多，计算量增大

2. 光滑着色 —— 不增加多边形，让亮度光滑过渡。

双线性亮度插值（Gouraud Shader）

Phong 明暗处理

优点：

• vs Gourand——相邻多边形之间的亮度过渡更自然。

• 能较好地模拟高光。

缺点：

• 计算量比 Gouraud 要大。

增量算法

优点：

• vs 平面着色——生成的图形真实感较好。

• vs Phong——快速，只需计算顶点的亮度，其余点通过插值得到。

缺点：

• 马赫带效应依然存在。

• 能比较好地模拟漫反射表面，但不能正确模拟高光。

纹理

光照模型生成的图形，表面太光滑，颜色单一，显得不真实。

贴纹理：为物体表面添加纹理的技术。

纹理分类

根据表现形式

1. 颜色纹理——光滑表面

比如刨光的木材表面的木纹、墙壁表面的装饰图案。 通过改变物体表面的颜色或亮度实现。

1. 几何纹理——粗糙表面

比如橘子皮表面的褶皱。 通过改变物体表面的微观几何结构实现。

1. 过程纹理——不规则、动态

比如水波、烟雾。 表现不规则的动态变化的自然景物。

颜色纹理

1. 定义纹理图案：纹理坐标 (s,t)

2. 定义纹理映射：建立纹理坐标 (s,t) 和物体表面点 (x,y,z) 的对应关系，把 (s,t) 的颜色值赋给 (x,y,z)

3. 把物体投影到屏幕

定义纹理图案

1. 离散法——用数字化图像定义。

2. 连续法——用数学函数表示。

建立映射

建立纹理坐标 (s,t) 和屏幕像素 (xs,ys) 的对应关系

凹凸纹理

对物体表面作微小扰动，从而产生凹凸不平的效果。

凹凸纹理实现

1. 对物体表面的每一个点 P(u,v)，沿该点的法向作位移 F(u,v)（对法向量作扰动），新表面位置：

1. 计算新表面的法向量

1. 计算亮度